Many applications require objects that are sheets, wafers, panels, or plates of conductive or conductively coated material. For many of these applications, the conductance of the entire object and/or the bulk conductance of the material are not the subject of inquiry. Sheet conductance is useful if the user wishes to know the conductance of the material as a sheet regardless of the dimensions of the material as a whole. This a function of the thickness and conductivity of the material and not dependent on the size of the plane of the material.

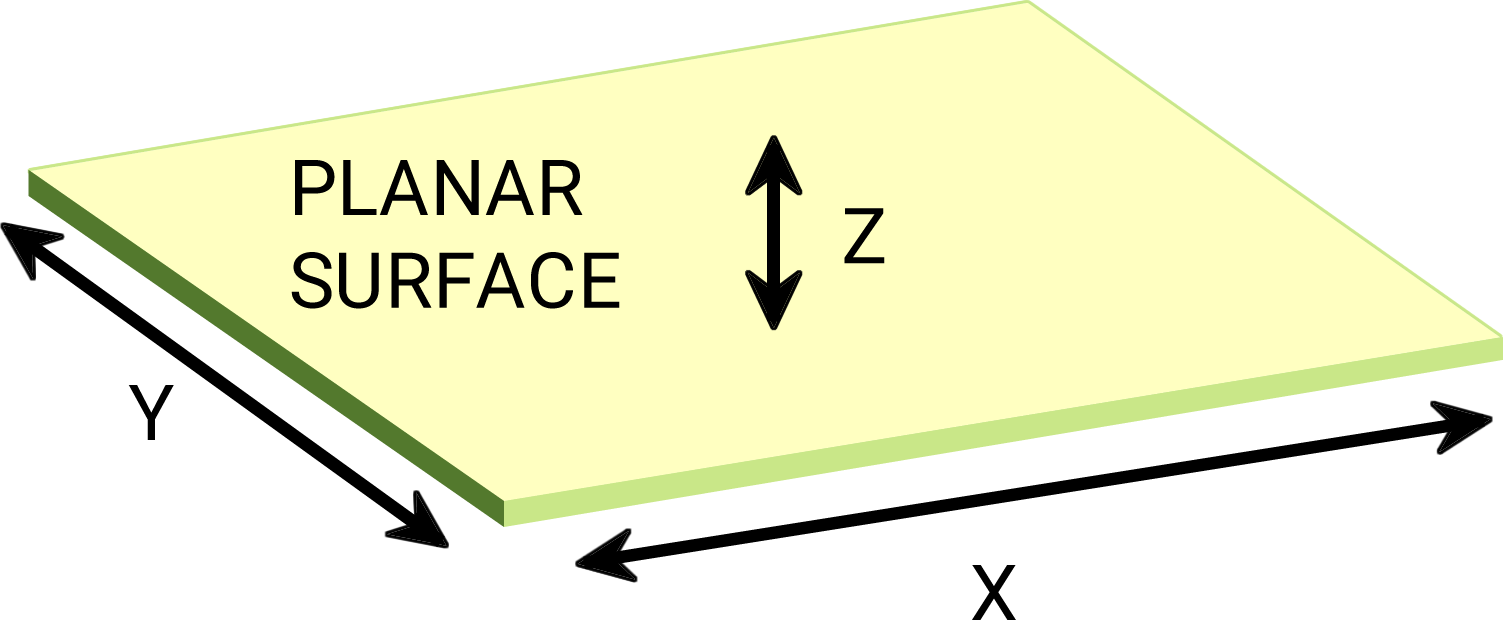
For use in these applications, sheet conductance (Cs) was created as a unit of measurement (G is the accepted symbol for sheet conductance, but Cs will be used in this discussion to avoid confusion). The inherent value of sheet conductance is that it is a measure of the electrical properties of a material independent of the xy dimensions.

Figure 1: Sheet conductance does not depend on the XY dimensions of the sheet

Many scientists, engineers, and technicians are comfortable thinking in terms of resistance as opposed to conductance. However, a compelling argument can be made for the benefits of thinking in terms of sheet conductance.

First, the baseline reading for sheet conductance is zero. Conversely, the baseline reading for sheet resistance is infinity, which is unwieldy. Imagine a coating process that starts with a nonconductive substrate, then gradually adds conductive material to the substrate. In this example, the meter’s first reading would be infinity. The next reading would be one increment away from infinity towards zero, which is still infinity.

For eddy current meters (all of which convert from sheet conductance to sheet resistance), the series of increments might be Overrange, 10,000, 5,000, 3,000, etc. These values—of course—are hyperbolic. For most applications, linear scales (such as result from sheet conductance readings) are much easier to work with than hyperbolic scales (see Figure 2).

Second, when thinking in sheet conductance, superposition (addition of the measurements of multiple distinct layers) is much easier. When measuring two samples, users can simply add the values together to get the combined sheet conductance of the material. Calculating the sheet resistance of two samples is more difficult, because the inverse of the readings must be calculated before addition.

Third, sheet conductance simply makes more sense. Think in terms of speed measurement: kilometers per hour is a much more practical, useful quantity than hours per kilometer. It would be similarly inconvenient to measure the thickness of a paint coating in units that represent the reciprocal of the coating thickness.

For these reasons, research- and production-oriented operators are encouraged to use sheet conductance rather than sheet resistance to quantify their products.

Figure 2: Relationship between thickness, sheet conductance, and sheet resistance

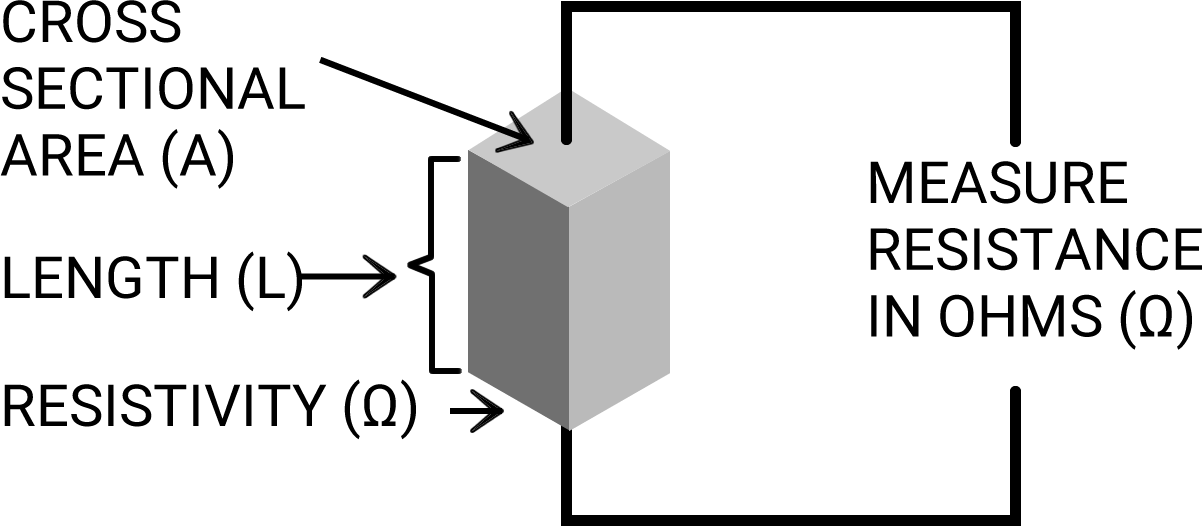
The electrical resistance (R) of an object is measured in Ohms and represented by the Greek letter Ω (omega). The resistance of a metal or a semiconductor can be measured using an ohmmeter (a common function on benchtop multimeters). The measurement of an object’s resistance can be taken with such a meter independent of the dimensions of the object or the object’s internal composition.

Figure 3: Resistance of an object

Therefore, we can say that electrical resistance (R) of an object is a result of three factors:

1. Cross-sectional area of an object (A)
2. Length of the object (L)
3. Intrinsic properties of the material the object is composed of—resistivity (ρ)

To determine the resistivity of various materials, objects composed of different materials but with the same dimensions were tested for their resistance. Table 1 shows the resistivities of some common materials.

Table 1: Resistivities of various materials

From these observations about the three factors of resistance, we conclude that resistance equals resistivity (ρ) times length (L), divided by area (A), as demonstrated by Figure 4 and Equation 1.

Figure 4: Resistance is a function of resistivity (ρ), length (L), and area (A)

Equation 1: Formula for resistance

R =ρxLA

In order to find the sheet resistance of an object, think of a square shape cut out of a doped silicon wafer, conductive film sheet, or a coated glass panel. We don’t want to have to worry about length and width along the entire plane of the material. This can be avoided by assuming a square shape. Now let’s describe the square as having a length (L), width (W), and thickness (T), as shown in Figure 5 below.

Figure 5: Sheet of resistive material

Next, let’s take our formula that relates length, area, and resistivity to resistance and transform it. This is done by substituting area (A) with width (W) times thickness (T).

Equation 2: Transforming resistance equation

R = ρxL A   ⇒   R = ρxL LxW

Finally, since the material in this example is a perfect square, we can substitute length (L) for width (W). This results in the equation: Sheet resistance (Rs) equals resistivity (ρ) divided by thickness (T).

Equation 3: Formula for sheet resistance

Let L =W and consider Rs

Rs = ρxL TxL   ⇒   Rs = ρ T

Conductance is the inverse, or reciprocal, of resistance. Therefore, sheet conductance is the reciprocal of sheet resistance, which means that sheet conductance (Cs) is equal to thickness divided by resistivity.

Equation 4: Equation for sheet conductance

Rs = ρ T   ⇒   Cs = 1 Rs   ⇒   Cs = T ρ

Example: Assume a silicon wafer of resistivity ρ =9.464 ohms-cm and thickness T = 0.0615 cm (aka 615 uM). Rs= ρ÷T. Sheet resistance = 9.464 ÷ 0.0615 = 153.9 ohms/square. Cs =T÷ρ. Sheet conductance = 0.0615 ÷ 9.464 = 0.0065 mhos/square.

Sheet conductance is measured in Siemens/Square. This can alternatively be written as Siemens/sq or Siemens-per-square. In addition, sheet conductance can be measured in mhos/square (“mhos” is “ohms” spelled backwards), mhos/sq, or mhos-per-square. Mhos/square can also be depicted by an upside down omega divided by a square. Very resistive layers are frequently measured in mMhos/square.

Eddy current meters work by introducing a current into the sensor’s inductor coil(s). This generates an oscillating magnetic field. When a conductive material is introduced into the magnetic field, a circular flow of electrons begins to move in the conductive layer due to magnetic induction. Eddy current technology earned its name because this flow of electrons is reminiscent of eddy current swirls in a body of water.

An eddy current instrument works by coupling the material to be tested to an amplitude stabilized oscillator. The power absorbed by the material in the oscillating magnetic field is proportional to the conductivity of the material. This power level is delivered as voltage to an analog-to-digital converter (ADC). This voltage is scaled from 0.0001 to 2.0000 voltage direct current (VDC). For a standard range meter, .0001 VDC is equal to .0001 Siemens/square.

The eddy current meter then scales this output digitally and displays the sheet conductance of the measured materials in Siemens/square or mhos/square.

In order to measure sheet conductance with a Delcom meter, the user must have access to Delcom software. The software might only need to be used once, but it is necessary to set the units of measurement to be displayed

1. Open the Delcom software.
2. Go to the main menu bar and choose Edit and then Units.
3. Select the radio button titled Sheet Conductance.

Figure 6: Setting units of measurement in the Delcom software

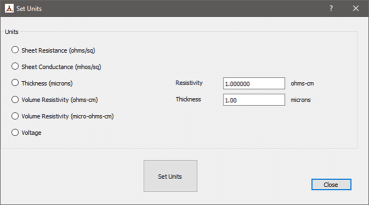
Upon completion of these steps, all subsequent readings by the meter on any of the user interfaces will be displayed in sheet conductance. This includes the LCD display, regardless of whether the PC is connected to the interface module or not. The user can revert to other units of measurement at any time by editing units under the settings menu.